When Will The Fall Colors Peak?

This week's Riddler Classic is about finding the max proportion of trees with fall colors.

It’s peak fall foliage season in Riddler Nation, where the trees change color in a rather particular way. Each tree independently begins changing color at a random time between the autumnal equinox and the winter solstice. Then, at a random later time for each tree — between when that tree’s leaves began changing color and the winter solstice — the leaves of that tree will all fall off at once.
At a certain time of year, the fraction of trees with changing leaves will peak. What is this maximal fraction?

I have two solutions to present. The first one uses discreet time intervals to then converge towards continuous time. While the second one is somewhat more classic.

First solution

Say you cut the time interval in \(N\) parts, hence \(t_k=\frac{k}{N}\). You can then count the proportion of trees that have their fall colors at \(t_k\):

• \(\frac{1}{N}\) turned to fall color between \(t_{k-1}\) and \(t_k\) ;
• out of the \(\frac{1}{N}\) that turned to fall color between \(t_{k-2}\) and \(t_{k-1}\), \(\frac{1}{N-k+1}\) lost their leaves, which gives \(\frac{1}{N}\frac{N-k}{N-k+1}\) ;
• etc.

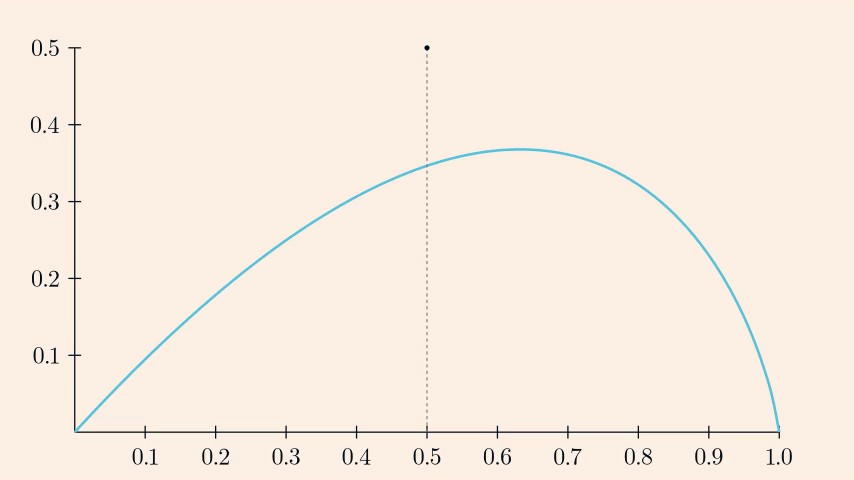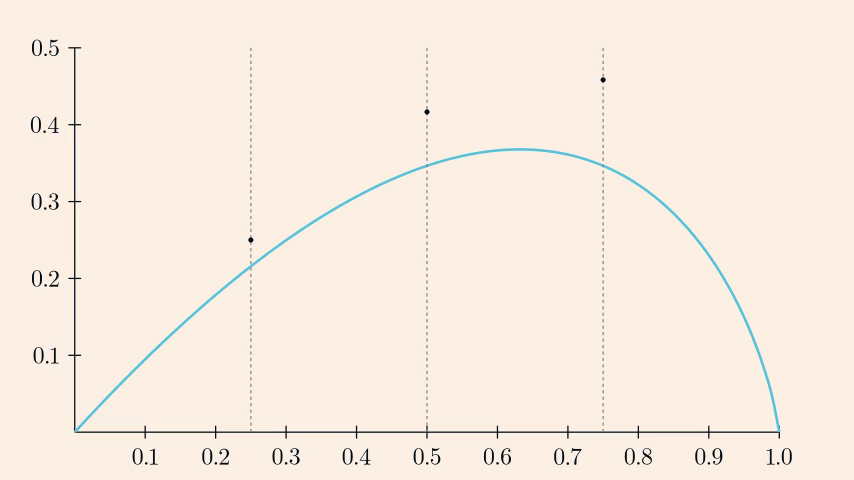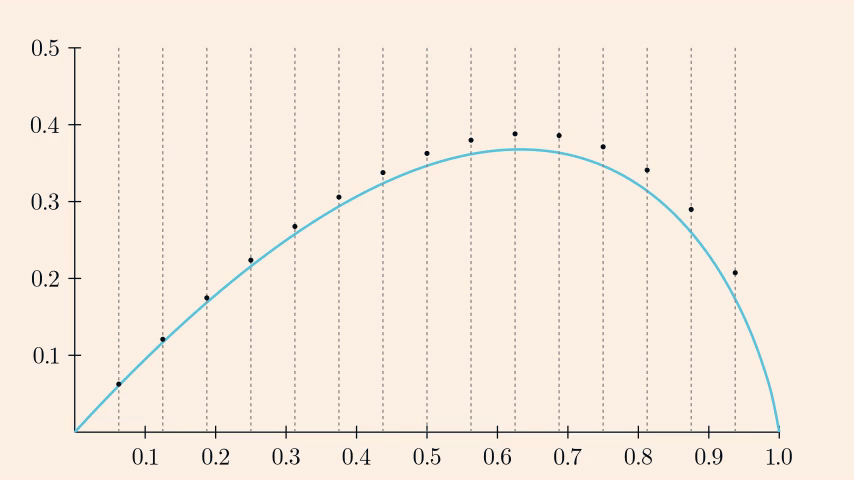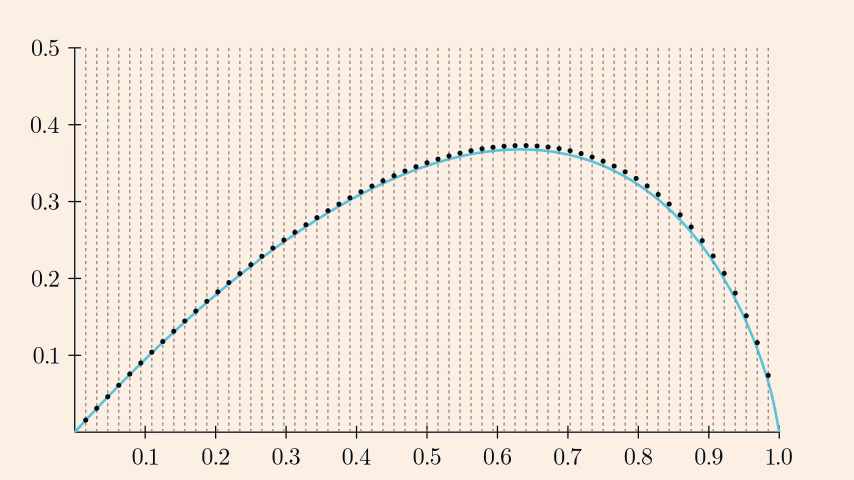
Eventually we have \[ \begin{align} p_k\ &=\ \frac{1}{N}\sum_{i=1}^k\frac{N-k}{N-i} \\ &=\ \frac{1}{N}\sum_{i=1}^k\frac{1-t_k}{1-t_i} \\ &\xrightarrow[N \to \infty]{} (1-t_k)\int_0^{t_k}\frac{1}{1-t} dt \ =\ (t_k-1)\ln(1-t_k). \end{align} \]

The rest of the computation is done in the second solution.

Second solution

Let us define \(C\sim\mathcal{U}([0,1])\) and \(F\sim\mathcal{U}([c,1])\) the r.v. representing the time a tree changes color, resp. looses its leaves.

So we have \[ \begin{align} \mathbb{P}\{C\le t\le F\}\ &=\ \mathbb{P}\{C\le t\}\,\mathbb{P}\{t\le F\ |\ C\le t\} \\ &=\ t\frac{1}{t}\int_0^t\mathbb{P}\{t\le F\ |\ C=c\}dc \\ &=\ \int_0^t\frac{1-t}{1-c}dc \\ &=\ (t-1)\ln(1-t)\,, \end{align} \] as found in the first section.

Now its a matter of differentiating and then finding the zero of the latter. \[ \frac{dp}{dt}\ =\ \ln(1-t)\ +\ 1\,, \] and \(\frac{dp}{dt}=0\) for \(t=1-\frac{1}{e}\). Hence the answer is \[ p(1-e^{-1})\ =\ \frac{1}{e}. \]