Can You Knock Down The Gates?

This week's Riddler Express is about finding the max horizontal velocity of a falling pole.

From the fantastical land of Central Earth comes a physics riddle that will break down your doors:
In an effort to break open the gates of the city Tinas Mirith, an army of orcs first tried using a battering ram, but to no avail. They next erected a 100-foot pole with a very massive weight at the top (i.e., the weight is much, much heavier than the rest of the pole). The pole is also anchored at the bottom, so that as the weight falls the entire pole rotates around its bottom without slipping.
How far away should the orcs position the vertical pole from the gates so that when the weight comes crashing down on the gates, its horizontal speed is as great as possible?

Here is my solution:

With \(\theta\) defining the angle between the pole and the vertical axis, we have \(E_p=mgL\cos\theta\) the potential energy of the mass.
Now with the law of conservation of energy, we have: \[ mgL\ =\ mgL\cos\theta\ +\ \frac{1}{2}mv^2. \]

Hence, its velocity is \(v=\sqrt{2gL(1-\cos\theta)}\) and its horizontal velocity is \[ v_x\ =\ \cos\theta\sqrt{2gL(1-\cos\theta)}. \]

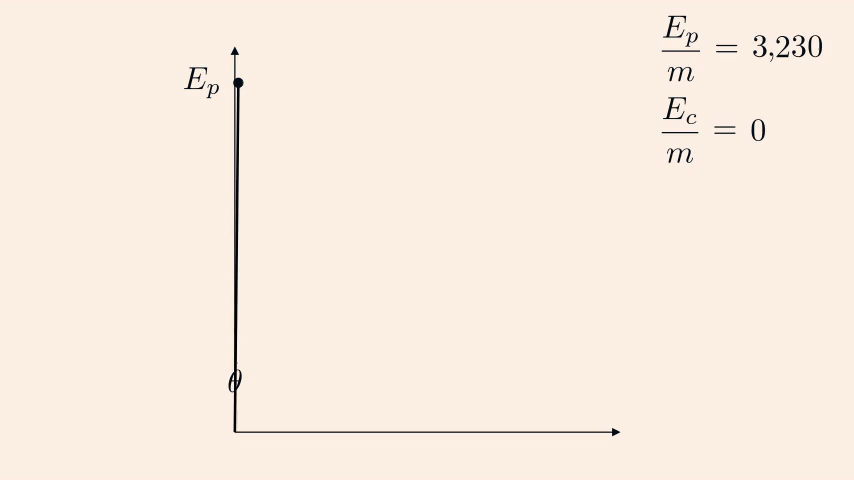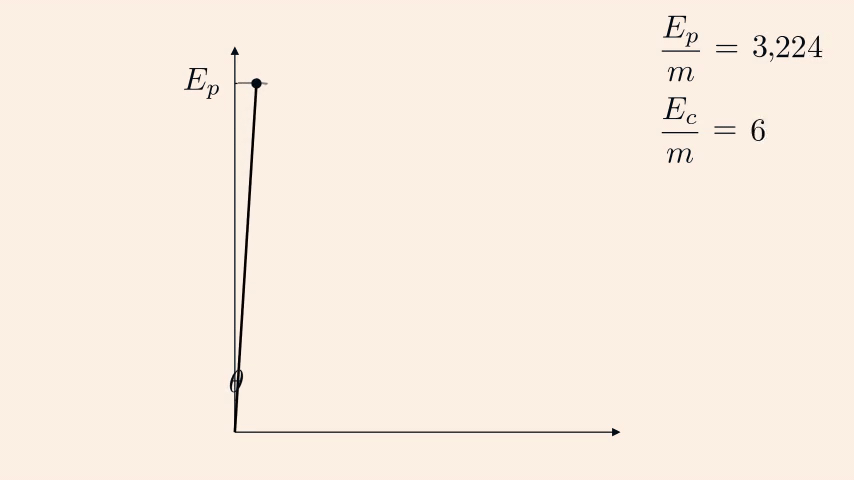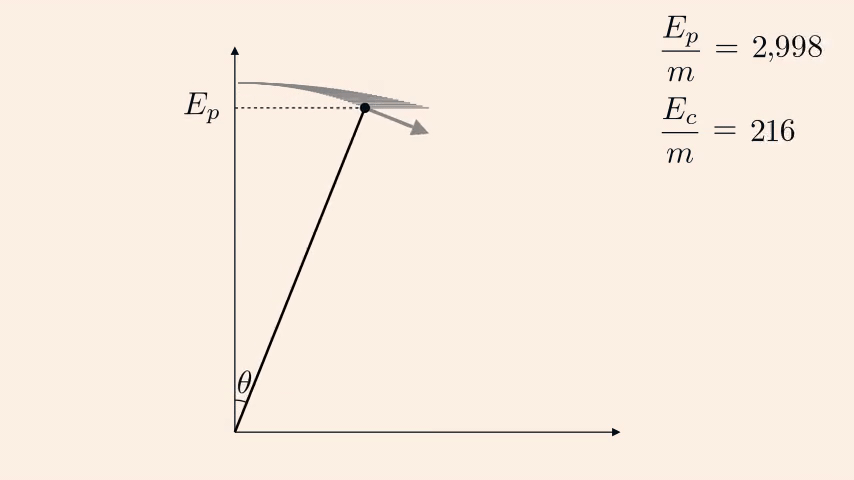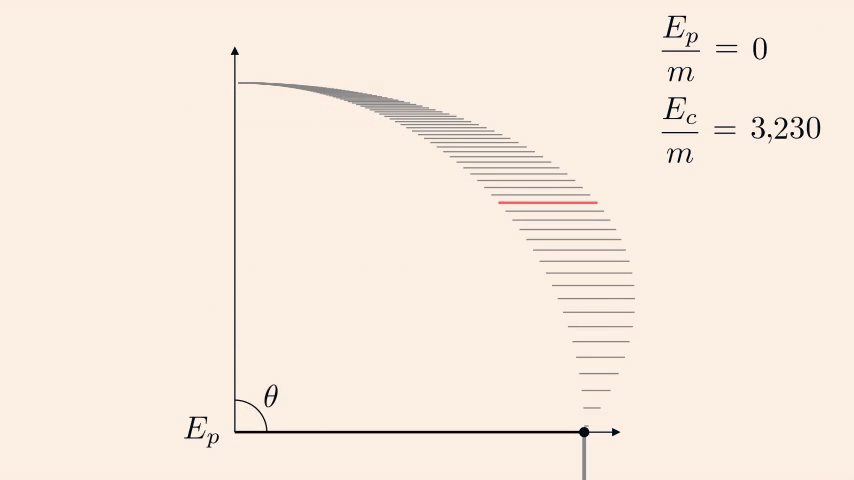
It is now easy to differientiate \(v_x\) with respect to \(\theta\) ; and the maximum horizontal velocity (zero of the derivative) is obtained for \(\cos\theta_m=\frac{2}{3}\).
So the optimal pole's distance to the gates is \[ \begin{align} L\sin\theta_m\ &=\ 100\frac{\sqrt 5}{3} \\ &\approx\ 74.5\ \text{feet}. \end{align} \]