Can You Fend Off The Alien Armada?

This week's Riddler Classic is about finding the max number of space fighters you can construct.

From James Anderson comes a puzzle to stave off galactic disaster:
The astronomers of Planet Xiddler are back in action! Unfortunately, this time they have used their telescopes to spot an armada of hostile alien warships on a direct course for Xiddler. The armada will be arriving in exactly 100 days. (Recall that, like Earth, there are 24 hours in a Xiddler day.)
Fortunately, Xiddler’s engineers have just completed construction of the planet’s first assembler, which is capable of producing any object. An assembler can be used to build a space fighter to defend the planet, which takes one hour to produce. An assembler can also be used to build another assembler (which, in turn, can build other space fighters or assemblers). However, building an assembler is more time-consuming, requiring six whole days. Also, you cannot use multiple assemblers to build one space fighter or assembler in a shorter period of time.
What is the greatest number of space fighters the Xiddlerian fleet can have when the alien armada arrives?

Let's tackle the problem by first computing the number of space fighters for small numbers of assemblers.
Then we will find a caveat on the general formula.
Enventually we can get a value for each valid number and find the solution.

A formula

The simplest case is if you want to get \(x=2^q\) assemblers. The first \(6n\) days you assemble your assemblers, then you have \(100-6n\) days left to assemble the space fighters. Which gives the number of space fighters at the end of the 100 days: \[ f(2^q)\ =\ (100-6n)\times 2^q\times 24. \]

Now what if you want to get 5 assemblers? The best strategy is to get 4 the first 12 days, then to use 1 to get the other one in 6 days, and the 3 left to already get some space fighters. The formula is \[ \begin{align} f(5)\ &=\ (100-2\times 6)\times 3\times 24 \\ &\qquad +\ (100-3\times 6)\times 2\times 24. \end{align} \]

In the general case, you have \(x=\sum_{i=1}^n2^{q_i}\), with \(q_i<q_j\) for \(i<j\), the formula is \[ \begin{align} f(x)\ &=\ 24\,(100-6q_n)\,(2^{q_n}-2^{q_{n-1}}) \\ \qquad &+\ 24\,\sum_{i=2}^{n-1}(100-6(q_n+n-i))\,(2^{q_i+1}-2^{q_{i-1}}) \\ \qquad &+ 24\,(100-6(q_n+n-1))\,2^{q_1+1}. \end{align} \]

Valid numbers only

Now if \(x=2^q\) assemblers, the biggest number I can get is for \(q=16\), which needs \(6\times16\) days to get. Indeed I would need 6 more days for more assemblers, but I have only four left.

So what is the equivalent in the general case? Well the last line of the formula tells me that I need \(6(q_n+n-1)\) days to get the last power of two of assemblers. And hence the total number of assemblers wanted. Which gives the condition \[ 6(q_n+n-1)\ <\ 100. \]

Code and graphic

First I write a function that gives me the list \((q_i)_{1\le i\le n}\).

                
def n2bin(n):
    res = []
    b = bin(n)[2:]
    for i, e in enumerate(b):
        if e == 1:
            res.append(len(b) - 1 - i)
    return res
                
                

Eventually the python code is simpler than the formula:

                    
def n_sf(n):
    res = 0
    b = n2bin(n)
    if (b[0] + len(b) - 1) * 6 >= 100:
        return 0
    t = 100 - 6 * b[0]
    for i, e in enumerate(b):
        if i == 0:
            sf = 2**e
        else:
            sf = 2 * 2**e
        if not i == len(b) - 1:
            sf -= 2 ** b[i + 1]
        res += t * sf
        t -= 6
    return res * 24
                
                

One can plot the result: number of space fighters as a function of number of assemblers. On the top in linear scale, on the bottom in log (base 2) scale.

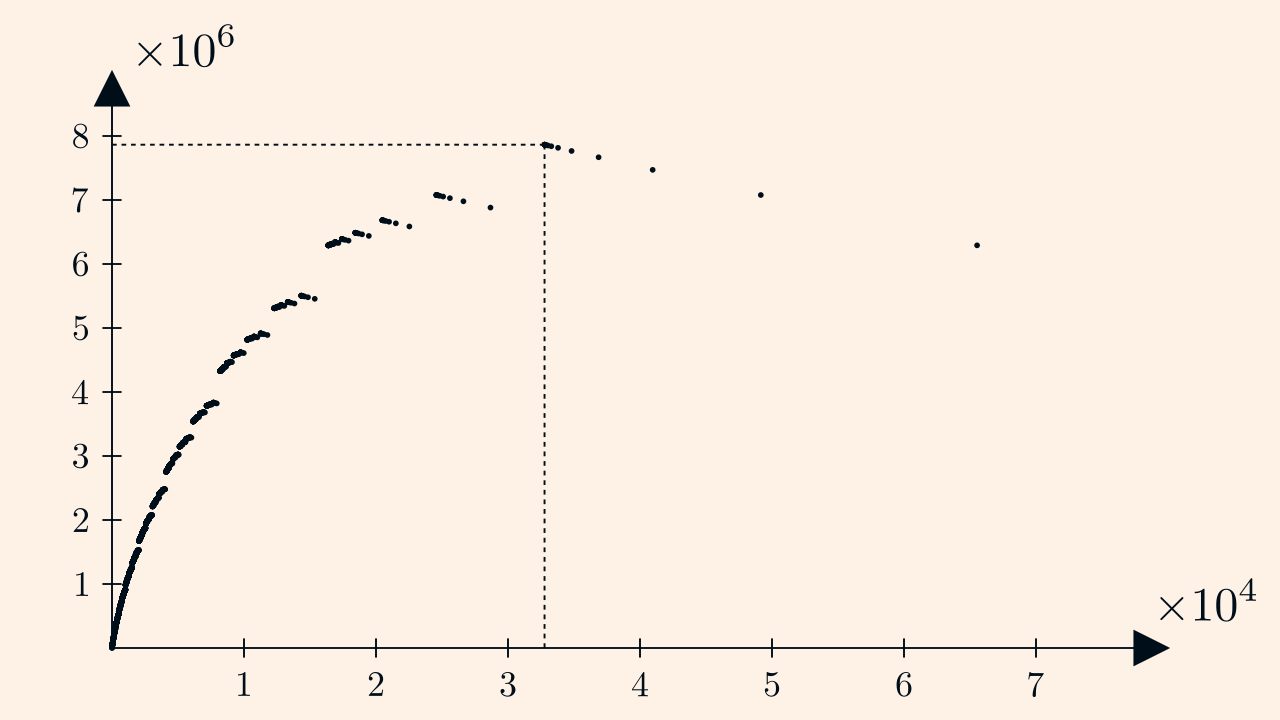
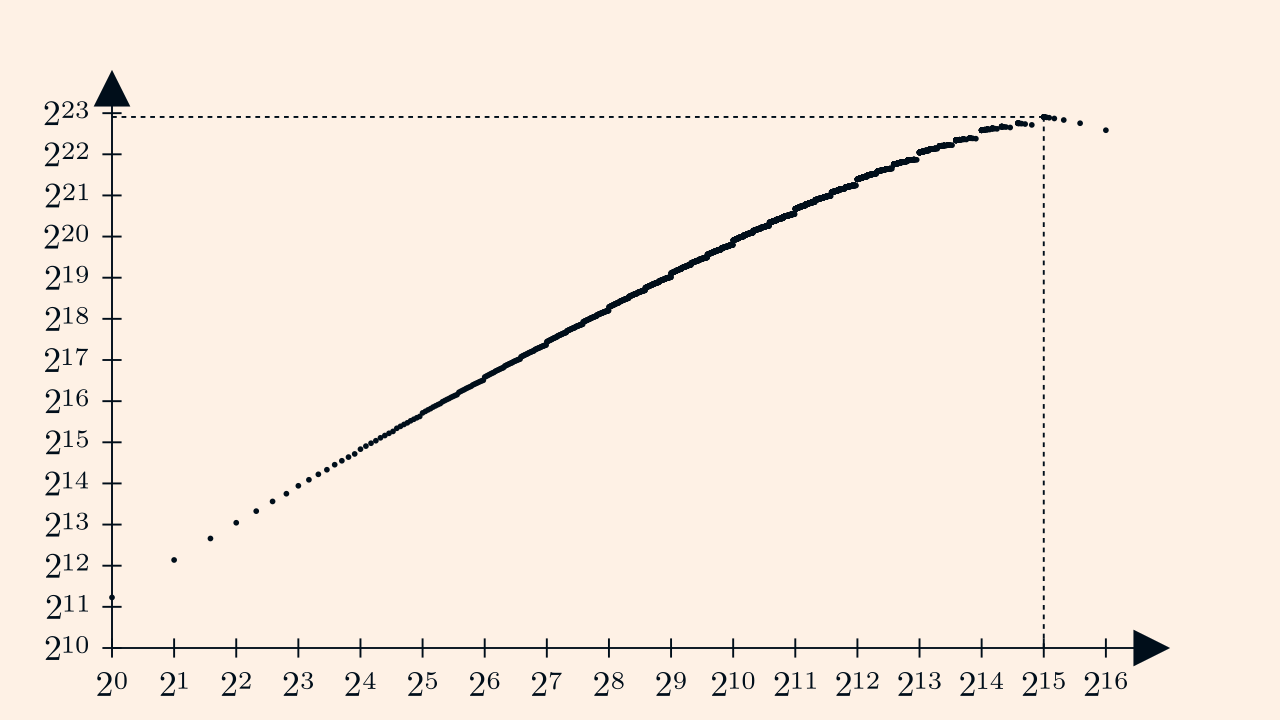
We can work with at most \(2^{16}\) assemblers, but the maximum is atteined for \(2^{15}\) assemblers.