Can You Crawl Around The Cone?

This week's Riddler Classic is about finding the geodesic on a cone:

Two ants named Geo and Desik are racing along the surface of a cone. The circular base of the cone has a radius of 2 meters and a slant height of 4 meters. Geo and Desik both start the race on the base, a distance of 1 meter away from its center.
The race’s finish is halfway up the cone, 90 degrees around the cone’s central axis from the start. A cone with a radius of 2 meters and a slant height of 4 meters. The starting point is halfway along a radius on the base. The finish point is halfway up the slant height, 90 degrees from the radius around the central axis.
Geo and Desik both want your help in strategizing for the race. What is the length of the shortest path from the start to the finish?

Here is my solution:

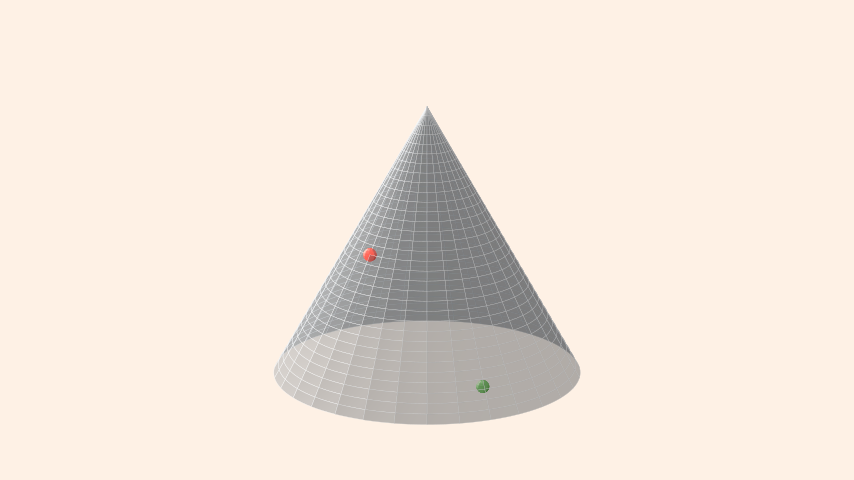
Let us first have a look at the 3D representation of the cone, with the green (resp. red) dot the start (resp. finish) point:

At this point, a good idea is to represent this cone in 2D, i.e. its net. From there, it's easy to see that one of the trajectory that minimises the distance is the addition of two lines: one going from the starting point to the edge of the base (blue line in the following sketch), the other one from the previous location to the finishing point (purple line).

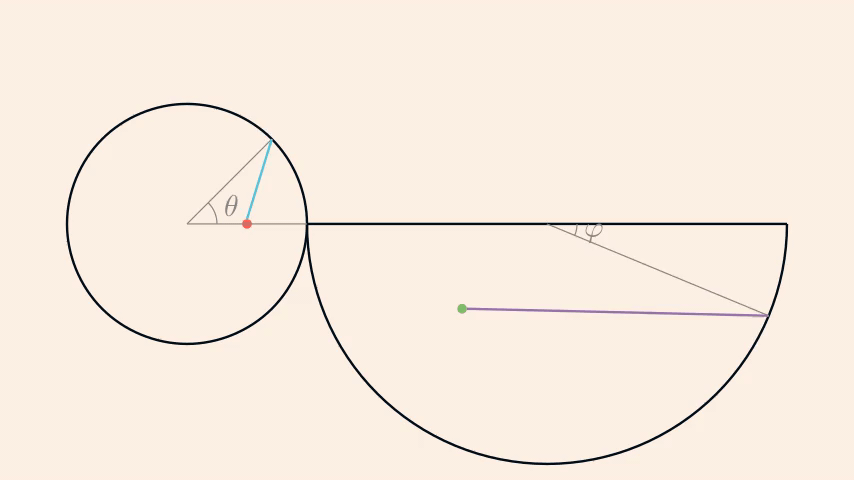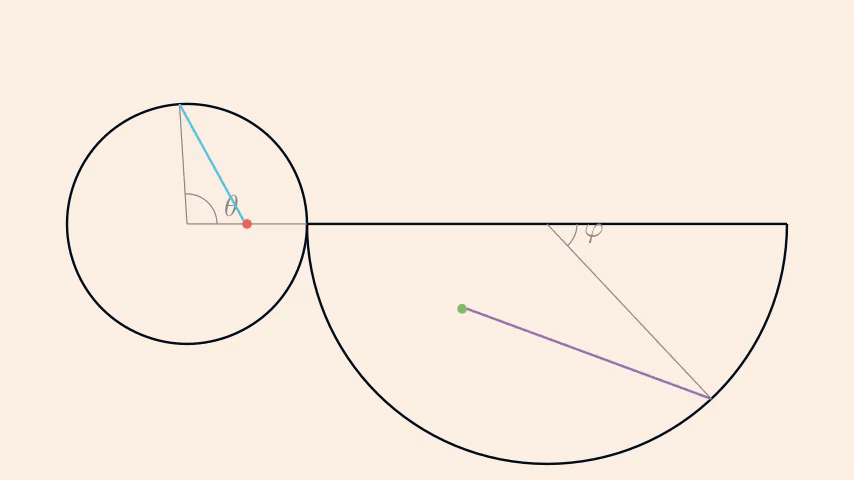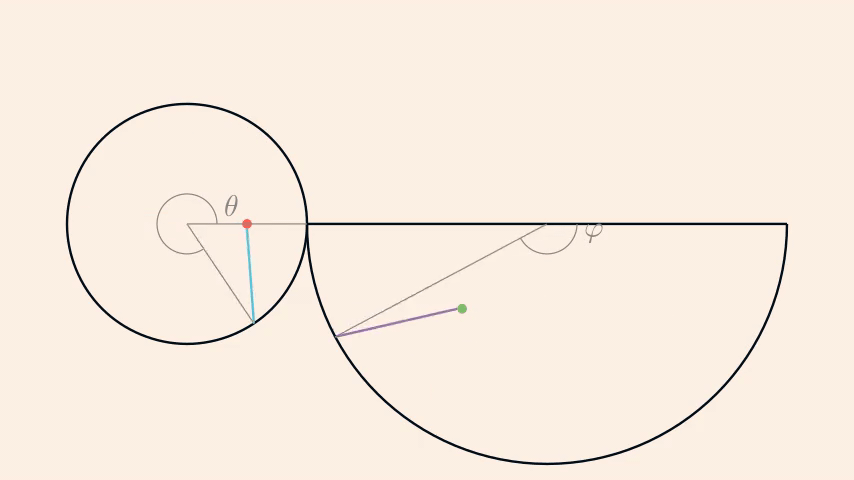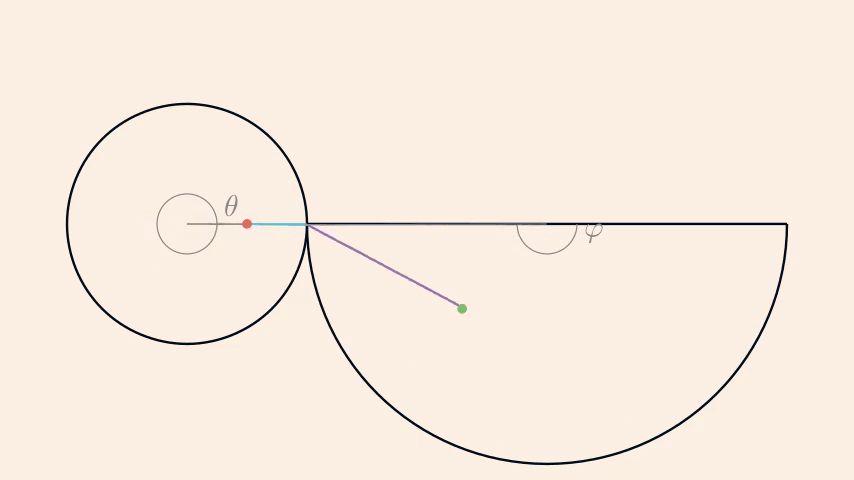
\(\theta\) and \(\varphi\) are related by \(\varphi=-\frac{\theta}{2}\).

Now it's just a matter of computing the sum of the lengths of the two lines, and finding the minimum value. Let us note \(d_1(\theta))\) (resp. \(d_2(\varphi)\)) the length of the blue (resp. purple) line. The starting point is located at \((1, 0)\), and the edge of the base at \((2\cos\theta, 2\sin\theta)\); then we have \[ \begin{align} d_1(\theta)\ &=\ \sqrt{(1-2\cos\theta)^2\ +\ (0-2\sin\theta)^2} \\ &=\ \sqrt{5\ -\ 4\cos\theta}. \end{align} \] And the length of the purple line is: \[ d_2(\varphi)\ =\ \sqrt{20\ +\ 8\sqrt{2}(\cos\varphi+\sin\varphi)}. \]

So the total length is \(d(\theta)=d_1(\theta)+d_2(-\frac{\theta}{2})\). Now to find its minimum on \(\theta\in[0,2\pi[\) you can just derivate and find its root (I'll spare you the calculations).
The minimum occurs at \(\theta=-\frac{\pi}{6}\), for a total length of \(3\sqrt{5-2\sqrt{3}}\).